BraveTiger
CH5. 머신러닝_회귀(2) 본문
파라미터 추정
: 비용함수를 최소화하는 파라미터 β를 찾는 것.
※ 비용함수(Cost function)
비용함수는 입력으로 받은 데이터를 모아서 오차를 계산하는 함수를 일컫는다. 입력으로 들어온 데이터를 기반으로 모든 데이터의 비용을 계산하는 방식으로 다음과 같은 수식을 갖는다.
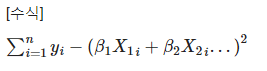
파라미터 추정 프로세스
파라미터 추정 프로세스

파라미터 추정 알고리즘
Algorithm: Least Squares Estimation Algorithm(최소제곱법)
- cost function of linear regression is convex: 전역 최적해가 존재(globally optimal solution exits)
- 오차를 최소화하는 회귀 계수를 추정하는 방

최소제곱법을 이용한 선형회귀 모델 예제
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
Area = [1380, 3120, 3520, 1130, 1030, 1720, 3920, 1490, 1860, 3430, 2000, 3660, 2500, 1220, 1390]
Value = [76, 216, 238, 69, 50, 119, 282, 81, 132, 228, 145, 251, 170, 71, 29]
plt.figure(figsize = (10, 8))
sns.regplot(Area, Value)
plt.xlabel("Area"); plt.ylabel("Value"); plt.title("Regreesion of Appraised Value vs Area");
#집 크기가 1 증가할 때마다 집 가격은 0.08 증가
print(f"Value = {np.polyfit(Area,Value,1)[0]: .2f}Area" + f"{np.polyfit(Area,Value,1)[1]: .2f}")
# 출력
Value = 0.08Area-29.59
파라미터 추정
파라미터에 대한 점추정
$Y_i = \beta_0 + \beta_1X_i + \epsilon_i$, $\epsilon ~ N(0, \sigma^2)$, $i = 1, 2, 3, ...n$
: 선형회귀모델에는 총 3가지 파라미터가 존재한다.

파라미터에 대한 구간추정
구간으로 추정하여 보다 유연한 정보를 제공

"""
# 선형회귀모델 가설검정 예제
# 가설 H0:B1 = 0 vs H1:B1 !=0
H1:B1 ==0: 기울기가 0이다.(귀무가설) -> 집 크기가 집가격에 유의미한 영향을 미치지 않는다다.
H1:B1 !=0: 기울기가 0이 아니다.(대립가설) -> 집 크기가 집가격에 유의미한 영향을 미친다.
"""
import statsmodels.api as sm
Area = sm.add_constant(Area)
model = sm.OLS(Value, Area)
result = model.fit()
print(result.summary())
"""
1. 파라미터는 무엇인가?//// x1, constant
2. 파라미터에 대한 점추정 값은 무엇인가?////x1 = 0.0779, constant = -29.5880
3. 파라미터에 대한 표준편차는 무엇인가?/////x1 = 0.004, constant = 10.657
4. t가 의미하는 것?/// t는 검정통계랑이다. 17.83
5. P > |t|가 의미하는 것? P-value 0.000
결론: β1 != 0 기울기가 0이 아니다. 즉 집크기(X)는 집가격(Y)에 유의미한 영향을 미친다.
"""
결론
1. 회귀 모델에서 파라미터를 추정하는 방법에 Least Squares Estimation Algorithm이 있다.
2. 실제값과 예측값의 오차 제곱합(RSS)이 최소가 되는 해를 구하는 방법으로 방정식이 어떤 형태인지를 알고 있을 때 방정의 회귀 계수 추정하는 데에 사용된다.
3. 파라미터가 유의한지 추정하는 방식은 점추정과 구간추정이 있다.
4. 파라미터 추정을 통해 얻을 수 있는 결과는 파라미터의 값(coef), 표준 오차(std err), 통계량(t), P-value를 통해 종속변수를 설명/예측하는 데 있어 설명변수 X가 유의미한지 추정할 수 있다.
'취업 준비 > AIVLE SCHOOL' 카테고리의 다른 글
| CH5. 머신러닝_LogisticRegression (0) | 2023.03.27 |
|---|---|
| CH5. 머신 러닝_KNeiborsClassfier (0) | 2023.03.27 |
| CH5. 머신러닝_회귀(1) (0) | 2023.03.06 |
| CH5. 머신러닝 - 머신러닝 모델 학습 (0) | 2023.03.06 |
| CH4. 데이터 수집5 - requests(GET, POST) (0) | 2023.02.27 |
Comments


